Catmull-Rom Spline
Catmull-Rom样条线是一种由四个控制点P0,P1,P2,P3定义的插值样条曲线(通过其控制点的曲线),曲线只绘制从P1到P2的部分。相比bezier曲线的优点是可以通过控制点,更加直观。
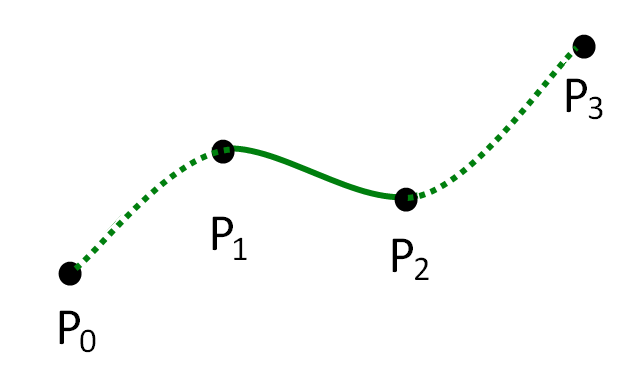
one segment of Catmull-Rom spline
如果我们想要绘制一条通过k个点的曲线,需要k+2个控制点,因为曲线绘制不会通过第一个和最后一个点,这两个额外的点可以自己任意选择,但它们会影响曲线形状。对于每一个在Pn到Pn+1点之间的曲线段,都由点Pn-1,Pn,Pn+1,Pn+2四个点计算得(1≤ n ≤k-1 )。当这些线段组合在一起时,就形成了一条连续的曲线,该曲线通过P1到Pk之间的所有点。

A smooth path
定义
假设 $P_i= \begin{bmatrix}x_i & y_i\end{bmatrix}^T$代表二维中的一个点,对于一段由 $P_0,P_1,P_2,P_3$和节点$t_0,t_1,t_2,t_3$定义的曲线段$C$,Catmull–Rom可以表示为:
\[q(t)=\frac {t_2-t}{t_2-t_1} B_1+\frac {t-t_1}{t_2-t_1} B_2\]其中
\[B_1=\frac {t_2-t}{t_2-t_0} A_1+\frac {t-t_0}{t_2-t_0} A_2\] \[B_2=\frac {t_3-t}{t_3-t_1} A_2+\frac {t-t_1}{t_3-t_1} A_3\] \[A_1=\frac {t_1-t}{t_1-t_0} p_0+\frac {t-t_0}{t_1-t_0} p_1\] \[A_2=\frac {t_2-t}{t_2-t_1} p_1+\frac {t-t_1}{t_2-t_1} p_2\] \[A_3=\frac {t_3-t}{t_3-t_2} p_2+\frac {t-t_2}{t_3-t_2} p_3\]其中
$t_i=t_{i-1}+\begin{Vmatrix}p_i-p_{i-1}\end{Vmatrix}^{\alpha}$ 以及 $t_0=0,i=1,2,3, and \ \alpha \in [0,1]$
解释
接下来解释这些定义以及公式的含义:
首先t代表去插值这条曲线的自变量,t0,t1,t2,t3分别为t位于p0,p1,p2,p3点时的数值。A1,A2,A3分别为点p0到p1,p1到p2,p2到p3的一维插值函数,即例如A1相当于lerp(p0,p1,(t-t0)/(t1-t0))。B1,B2为A1到A2,A2到A3的插值函数,例如B1相当于lerp(A1,A2,(t-t0)/(t2-t0)),最终曲线段C为B1到B2的插值结果,就是lerp(B1,B2,(t-t1)/(t2-t1)),即最后C会是三次曲线函数。
假设t1=1,t2=2,t3=3,下图中橙色虚线为A1,A2,A3,蓝色线为B1,绿色线为B2,黑色线为C。
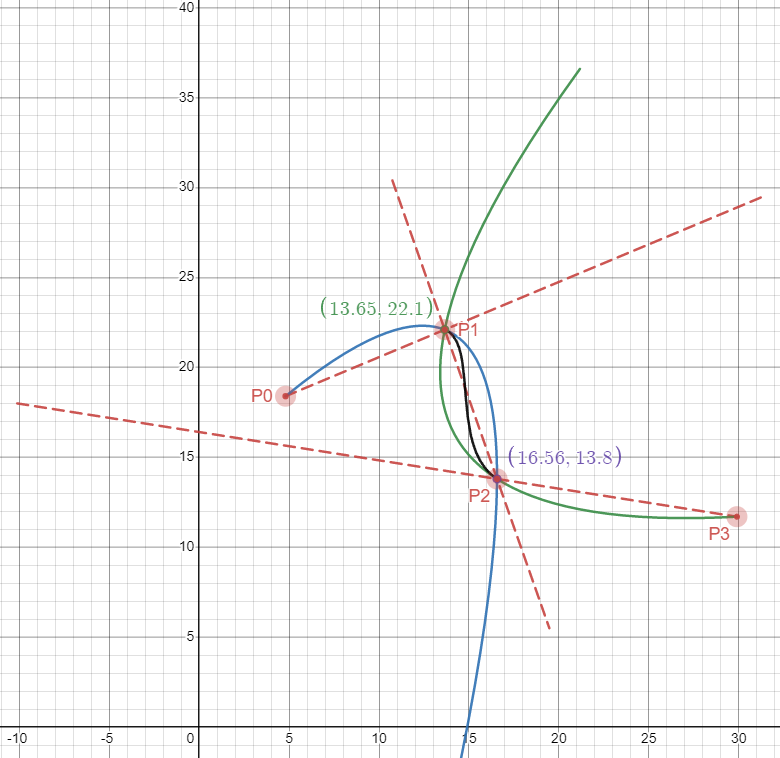
$t_i=t_{i-1}+\begin{Vmatrix}p_i-p_{i-1}\end{Vmatrix}^{\alpha}$中 $\alpha$是控制样条线形状的参数,当 $\alpha=0$时t1=1,t2=2,t3=3,正如上图所示,此时得到的曲线是标准的uniform Catmull-Rom样条曲线,当$\alpha=1$,结果被称为chordal atmull-Rom spline,当$\alpha=0.5$,结果为centripetal Catmull–Rom spline。
下图是三种样条曲线节点参数的变化尺度,可以看到uniform是均匀变化的,每次加1。

下图是当 $\alpha$取0-1间不同值时样条线的变化。


可以看到当$\alpha$取0时曲线会产生自相交,而当$\alpha$取1时曲线会偏离直线路径较远,因此实际使用中常选用Centripetal cat-mull样条线。
这里提供了交互式示例演示了 Catmull-Rom 样条和这些参数。
计算应用
用上面的方程计算曲线可能相当不方便,通常情况下,使用预计算好的常数比较好,那么p1和p2之间的曲线段就可以用下面的方程表示,
\[p(t)=at^3+bt^2+ct+d,\]$t \in [0,1],p(0)=p_1,p(1)=p_2$.另一种定义方式$p(t)=q(t_1+t(t_2-t_1)).$
可得,
$p’(t)=3at^2+2bt+c=(t_2-t_1)q’(t_1+t(t_2-t_1)).$
现在我们有,
$p(0)=q(t_1)=p_1=d,$
$p(1)=q(t_2)=p_2=a+b+c+d,$
$p’(0)=(t_2-t_1)q’(t_1)=m_1=c,$
$p’(1)=(t_2-t_1)q’(t_2)=m_2=3a+2b+c,$
其中m1,m2代表p1,p2处的切线,通过以上四个公式求解a,b,c,d得,
$a=2p_1-2p_2+m_1+m_2,$
b=$-3p_1+3p_2-2m_1-m_2,$
$c=m_1,$
$d=p_1$
至此,我们只需要确定m1和m2,那就需要求q的导数,得到,
$q’(t_1)=\frac {p_1-p_0}{t_1-t_0}-\frac {p_2-p_0}{t_2-t_0}+\frac {p_2-p_1}{t_2-t_1},$
$q’(t_2)=\frac {p_2-p_1}{t_2-t_1}-\frac {p_3-p_1}{t_3-t_1}+\frac {p_3-p_2}{t_3-t_2},$
所以m1,m2为,
$m_1=(t_2-t_1)(\frac {p_1-p_0}{t_1-t_0}-\frac {p_2-p_0}{t_2-t_0}+\frac {p_2-p_1}{t_2-t_1})$
$m_2=(t_2-t_1)(\frac {p_2-p_1}{t_2-t_1}-\frac {p_3-p_1}{t_3-t_1}+\frac {p_3-p_2}{t_3-t_2})$
至此我们得到了三次曲线中的四个参数a,b,c,d,可以快速地插值曲线。
参考文章:
Smooth Paths Using Catmull-Rom Splines
Centripetal Catmull–Rom spline